Proyecto - Portada CD - Relaciones Geométricas Básicas Y Diseño

Este proyecto parte de la siguiente premisa: Realizar un estudio de diseño sobre las transformaciones geométricas básicas. Un estudio de los grupos de transformaciones (Proporción, escala, semejanza, homotecia, giros, traslaciones y simetrías). Un ejemplo de un trabajo puede ser el teorema Bravais, que abarca los conceptos de simetría, identidad y giro. O bien, un diseño sobre la proporción aurea y su aplicación a la estética. Los fundamentos científicos del número de oro.

Mi enfoque sobre este proyecto es el siguiente: Partir de la portada de un cd de música (Gojira, ‘Form Mars To Sirius’), y elaborar una portada alternativa basada en animales marinos formados por geometrías básicas (Tangram), realizando un análisis matemático de las relaciones entre las formas.

1.  Apartado Diseño.

Portada original del grupo (Joe Duplantier).

Diseño personal de portada.

2. Apartado matemático.

- Intro: Los triángulos de color verde (1er apartado) explican la relación de homotecia, proporción y escala. Los triángulos de color rojo (2º apartado) explican la simetría central y la razón de semejanza. Las figuras en naranja (3er apartado) explican el teorema de Bravais (Simetría axial, identidad y giro).

- Homotecia, proporción,  escala y Thales.

El triángulo 1 y el 2 están relacionados mediante el centro de homotecia O1, lo cual quiere decir que sus segmentos relativos son paralelos y proporcionales (a/a’=b/b’=k) y que las dimensiones del triángulo 2 están escaladas con respecto a las del triángulo 1 (En este caso k=1/4=0.5). (Más adelante aparecerá una homotecia de razón negativa, cuando lleguemos a la simetría central).

La relación de proporcionalidad entre ambos triángulos puede definirse de la siguiente manera: O1A/O1A’=O1B/ O1B’=k, o también: O1A’/A’B’=O1A/ AB=k.

Los triángulos 1 y 3 están en posición de Thales.  Por este motivo son proporcionales y homotéticos entre sí. La peculiaridad es que ambos tienen un ángulo, un vértice en común, y este también coincide con el centro de homotecia  (B≡B’’≡O2).

Al trabajar con triángulos, también podemos hablar del criterio de semejanza. En esta imagen los triángulos 1, 2 y 3 son semejantes entre sí. Los criterios de semejanza aparecen a continuación detallados, al hablar de la simetría central.

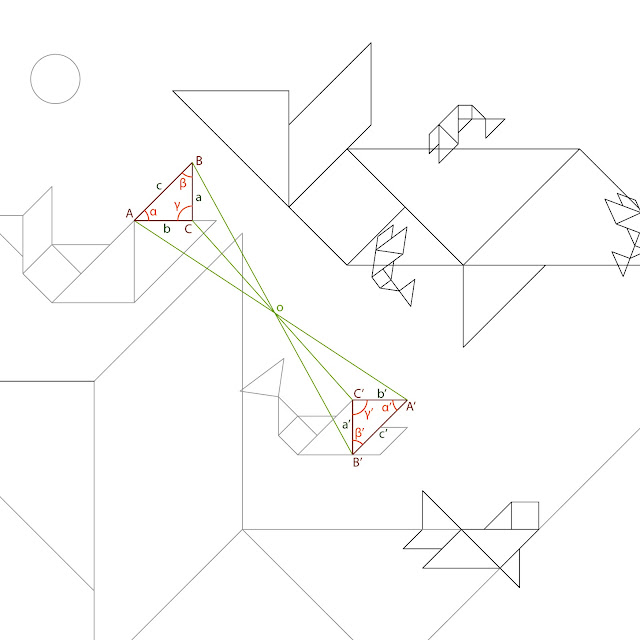
- Simetría central y criterio de semejanza.

Ambos triángulos están vinculados por una simetría central de centro en el punto O.  A y A’ son puntos homólogos ya que O es el punto medio del segmento que los une a ambos. De igual modo B y B’ o C y C’ también son puntos homólogos ya que OA=OA’, OB=OB’ y OC=OC’.

En una simetría central, los segmentos homólogos son iguales (a=a’, b=b’ y c=c’) y la medida de los ángulos correspondientes también son iguales (α=α’, β=β’ y γ=γ’).

Son triángulos homotéticos (Con centro de homotecia en O). La razón homotética que relaciona el segundo triángulo con respecto al primero es -1/1.

Ambos triángulos también son semejantes. Se llama criterio de semejanza de dos triángulos a las de condiciones tales que si se cumplen, tendremos la seguridad de que los triángulos son semejantes:

- Primer criterio: Dos triángulos son semejantes si tienen dos pares de ángulos respectivamente iguales (α=α’, β=β’ y γ=γ’).

- Segundo criterio: Dos triángulos son semejantes si sus lados son proporcionales (a/a’=b/b’=c/c’).

-Tercer criterio: Dos triángulos son semejantes si tienen un ángulo igual y los lados que lo forman son proporcionales (α= α’ y a/a’=b/b’).

- Teorema De Bravais (Simetría axial, identidad y giro).

Las tres figuras forman grupo.  La figura 2 es simétrica a la figura 1 mediante el eje 1 de simetría axial. La fig. 3 es simétrica a la  fig. 2 mediante el eje 2 de simetría. El teorema de Bravais demuestra como mediante un giro podemos obtener a partir de la fig. 1, la. fig 3, siendo el centro de giro (O) la intersección de los ejes de simetría 1 y 2.

En una simetría axial para hallar el punto simétrico (A’) de un punto (A), se traza una recta (r) perpendicular al eje de simetría (Eje1) que pase por el punto (A). La intersección entre esta recta (r) y el eje (Eje1), produce un punto (P). Partiendo de este punto (P) sobre la recta (r) llevamos la distancia que hay entre el punto del que partíamos (A) y el punto intersección (P). De tal forma que AP = PA’ y A’Q=QA’’.

Un Movimiento es una transformación (Una correspondencia de puntos, A-A’’ y B-B’’) en la que la forma y tamaño de las figuras resultan invariables. Las simetrías (A-A’ y B-B’ o A’-A’’ y B’-B’’) se consideran movimientos inversos porque no conservan la orientación de la figuras. El movimiento de la fig. 3 con respecto a la fig. 1, es un movimiento negativo (Giro en el sentido de las agujas del reloj) y directo (Este desplazamiento conserva el sentido de los ángulos).